Attention, plusieurs réponses sont possibles !!!
1. Soit l’intensité de courant i1(t)
= 3![]() sin (w t + 0,45). Quel est
le nombre complexe I
sin (w t + 0,45). Quel est
le nombre complexe I
1.1. I1= [3
; 0,45 rad]
1.2. I1= [3 ; 0,45 rad]
1.3. I1= [3
; 25,8°]
1.4. I1= [3 ; 0,45 °]
2. Soit le nombre complexe I2 représentant une intensité sinusoïdale de courant i2(t).
I2= [0,5 ; 30°]. Quelle est l’expression de i2(t) ?p/6)2.1. i2(t) = 0,5 sin (w t + 30)
2.2. i2(t) = 0,5
sin (w t + 30)
2.3. i2(t) = 0,5 sin (w t +
2.4. i2(t) = 0,5![]() sin (w t +
p/6)
sin (w t +
p/6)
3. Soit le nombre complexe Z1 = 3 + 4j. Quel est l’écriture trigonométrique de Z1 ?
3.1. Z1 = [5 ; 0,927 rad]
3.2. Z1 = [5 ; 1,33 rad]
3.3. Z1 = [5 ; 76,4 °]
3.4. Z1 = [5 ; 1,33 °]
4.Soit le nombre complexe Z2 = [10 ; p/4 rad]. Quelle est l’écriture algébrique de Z2 ?
4.1. Z2 = 10 + 0,14 j
4.2. Z2 = 7,07 + 7,07 j
5. On donne U1 = 3 + 4j et U2 = 5 – 7j. Calculer U1 + U2 .
5.1. U1 + U2 = 8 + 11j
5.2. U1 + U2 = 8 – 3j
6. On donne U1 = [4 V ; 0 °] et U2 = [7 V ; 45 °]. Calculer U1 + U2 .
6.1. U1 + U2 = [11 V ; 45 °]
6.2. U1 + U2 = [10,3 V ; 28,9 °]
6.3. U1 + U2 = 8,95 + 4,95j
7. Soient les nombres complexes Z1 = [3 ; 45 °] et Z2 = [7 ; 0 °]. Calculer Z1 x Z2 .
7.1. Z1 x Z2 = [21 ; 0°]
7.2. Z1 x Z2 = [10 ; 45°]
7.3. Z1 x Z2 = [21 ; 45°]
7.4. Z1 x Z2 = [10 ; 0°]
8. Soient les nombres complexes Z1 = 3 + 2j et Z2 = 1 – 4j. Calculer Z1 x Z2 .
8.1. Z1 x Z2 = 11 – 10j
8.2. Z1 x Z2 = [14,9 ; – 42,3°]
8.3. Z1 x Z2 = [7,7 ; – 42,3°]
8.4.Z1 x Z2 = [14,9 ; – 190°]
9. Soient les nombres complexes Z1 = [12 ; 45 °] et Z2 = [3 ; 12 °]. CalculerZ1 / Z2 .
9.1. Z1 / Z2 = [4 ; 3,75°]
9.2. Z1 / Z2 = [4 ; 33°]
9.3. Z1 / Z2 = [15 ; 57°]
9.4. Z1 / Z2 = [9 ; 3,75°]
10. Soient les nombres complexes Z1 = 3 + 4j et Z2 = 1 – 2j. Calculer Z1 / Z2 .
10.1. Z1 / Z2 = – 1 + 2j
10.2. Z1 / Z2 = [1,73 ; – 63°]
10.3. Z1 / Z2 = 3 – 2j
10.4. Z1 / Z2 = [2,24 ; 116,5 °]
11. Un dipôle est soumis à une tension sinusoïdale de valeur efficace 15 V. Il est traversé par un courant sinusoïdal d’intensité efficace 2,5 A. Quel est le module Z de l’impédance complexe de ce dipôle ?
W11.1. Z = 37,5
11.2. Z = 6
W11.3. Z = 137 m
W12. La tension aux bornes d’un dipôle passif est en retard de 30° par rapport à l’intensité du courant qui le traverse. Quel est l’argument
j de l’impédance complexe de ce dipôle ?12.1.
j = 30°12.2.
j = - 30°
13. Un dipôle est soumis à une tension sinusoïdale u(t) de valeur efficace U = 12 V. Il est traversé par un courant sinusoïdal dont la valeur efficace de l’intensité i(t) est I = 4 A. La tension u(t) est en avance de 60° sur i(t). Quelle est l’impédance complexe Z de ce dipôle ?
13.1. Z = 1,5 - 2,6j
13.2. Z = 1,5 + 2,6j
13.3. Z = -2,86 - 0,91j
14. La tension aux bornes d’un dipôle
est u(t) = 20 ![]() sin (314t). L’impédance complexe
de ce dipôle est Z = 4 + 3j. Quelle est l’expression de l’intensité
instantanée i(t) du courant qui traverse le dipôle ?
sin (314t). L’impédance complexe
de ce dipôle est Z = 4 + 3j. Quelle est l’expression de l’intensité
instantanée i(t) du courant qui traverse le dipôle ?
14.1. i(t) = 4 sin (314t - 0,644)
14.2. i(t) = 4
sin (314t - 0,644)
14.3. i(t) = 100
sin (314t + 0,644)
15. Une résistance de 100
W est traversée par un courant d’intensité (en mA) i(t) = 3015.1 U = 3
15.2. U = 2,6 + 1,5j
15.3. U = [3000 ; p/6]
16. A la fréquence f, le module de l’impédance complexe d’un condensateur de capacité C = 25 mF est proche de 127
W. Quelle est la valeur de la fréquence f ?16.1. f = 3,13.10-8 Hz
16.2. f = 50 Hz
16.3. f = 809 kHz
17. Un dipôle soumis à la tension u(t) = 4
![]() sin (314t + 0,524) est traversé par un courant
d’intensité i(t) = 0,127
sin (314t + 0,524) est traversé par un courant
d’intensité i(t) = 0,127 ![]() sin (314t - 1,047).
Ce dipôle est :
sin (314t - 1,047).
Ce dipôle est :
W17.1. une résistance R = 31,5
17.2. une inductance L = 0,1 H
17.3. une inductance L = 0,1 mH
17.4. un condensateur C = 0,1 F
18. Pour la fréquence f = 50Hz, quelle l’impédance complexe équivalente du dipôle ?
18.1. Z = 47 + 63,2j
18.2. Z = 47 - 0,415j
![]()
19. Un dipôle est constitué d’une association série de 2 dipôles élémentaires. A la fréquence 100 Hz, l’impédance complexe de ce dipôle est Z = 50 + 37j. Ce dipôle est constitué d’une association série :
19.1. d’une résistance et d’une inductance
19.2. d’une résistance et d’un condensateur
19.3. d’une inductance et d’un condensateur
20. A la fréquence 100 Hz, quelle est l’impédance
complexe Z de ce dipôle ?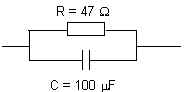
20.1. Z = 47 - 15,9j
20.2. Z = 4,83 - 14,3j
20.3. Z = 47 + 15,9j
21. Calculer U2.
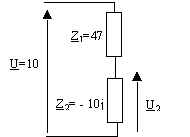
21.1. U2 = 20 - 97j
21.2. U2 = 0,433 - 2,04j
21.3. U2 = 9,6 - 2j
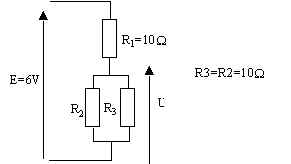
22. En utilisant la relation du diviseur de tension, calculer la valeur de U ?
22.1. U = 2 V
22.2. U = 3 V
22.3. La relation du diviseur de tension ne permet pas de calculer U
23. Un dipôle actif linéaire fournit à
vide une tension u(t) = 12 ![]() sin (314t +
p/4). Quel est l’élément du modèle équivalent de Thévenin que l’on peut
déterminer ?
sin (314t +
p/4). Quel est l’élément du modèle équivalent de Thévenin que l’on peut
déterminer ?
23.1. U0 = 8,49 (1 + j)
23.2. Z0 = 8,49 (1 + j)
23.3. Ni U0, ni Z0
24. On donne U = 10, Z1 = 10j, Z2 = 10. Déterminer les éléments du modèle équivalent de Thévenin du dipôle AB.
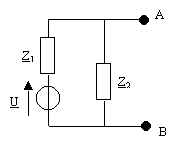
24.1. (U0 = 5 - 5j ; Z0 = 10 + 10j)
24.2. (U0 = 5 - 5j ; Z0 = 5 + 5j)
24.3. (U0 = 10 ; Z0 = 5 + 5j)
24.4. (U0 = 10 ; Z0 = 10 + 10j)
25. On donne U = 2, Z1 = 10j, Z2 = - 10j et Z3 = 10. Déterminer les éléments du modèle équivalent de Thévenin du dipôle AB.
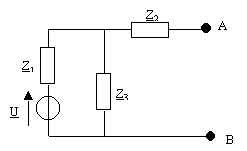
25.1. (U0 = 1 - 1j ; Z0 = 5 + 5j)
25.2. (U0 = 2 ; Z0 = 5 + 5j)
25.3. (U0 = 1 - 1j ; Z0 = 5 - 5j)
25.4. (U0 = 2 ; Z0 = 5 - 5j)
26. On donne U1 = 9, U2 = [6 ; p/2], Z1 = 10, Z2 = 10 et Z3 = 10. Quelle est la valeur de la tension complexe U ?
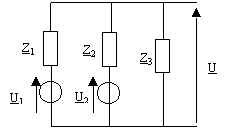
26.1. U = 15
26.2. U = 3 + 2j
26.3. U = 5